In electronics, a logic gate is an idealized or physical device implementing a boolean function that is, it performs a logical operation on one or more logical inputs, and produces a single logical output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device.
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their logical variables (Enderton,
2001). In particular, truth tables can be used to tell whether a
propositional expression is true for all legitimate input values, that
is, logically valid.
A
schematic, or
schematic diagram, is a representation of the elements of a
system using abstract, graphic
symbols
rather than realistic pictures. A schematic usually omits all details
that are not relevant to the information the schematic is intended to
convey, and may add unrealistic elements that aid comprehension. For
example, a subway map intended for riders may represent a subway station
with a dot; the dot doesn't resemble the actual station at all but
gives the viewer information without unnecessary visual clutter. A
schematic diagram of a chemical process uses symbols to represent the
vessels, piping, valves, pumps, and other equipment of the system,
emphasizing their interconnection paths and suppressing physical
details. In an electronic
circuit diagram,
the layout of the symbols may not resemble the layout in the physical
circuit. In the schematic diagram, the symbolic elements are arranged to
be more easily interpreted by the viewer.
Logic Gates and Truth Tables
| Type |
Distinctive shape |
Rectangular shape |
Boolean algebra between A & B |
Truth table |
|---|
| AND |
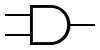 |
 |
 or or  & &  |
| INPUT |
OUTPUT |
| A |
B |
A AND B |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
| OR |
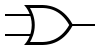 |
 |
 |
| INPUT |
OUTPUT |
| A |
B |
A OR B |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
|
| NOT |
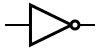 |
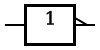 |
 or ~ or ~ |
| INPUT |
OUTPUT |
| A |
NOT A |
| 0 |
1 |
| 1 |
0 |
|
| NAND |
 |
 |
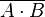 or or 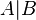 |
| INPUT |
OUTPUT |
| A |
B |
A NAND B |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
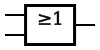
| NOR |
 |
 |
 or or  |
| INPUT |
OUTPUT |
| A |
B |
A NOR B |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
|
|
| XOR |
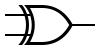 |
 |
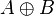 |
| INPUT |
OUTPUT |
| A |
B |
A XOR B |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
| XNOR |
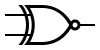 |
 |
 or or  |
| INPUT |
OUTPUT |
| A |
B |
A XNOR B |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
References: http://en.wikipedia.org/wiki/List_of_7400_series_integrated_circuits
http://electronicsclub.info/74series.htm



 or
or  &
& 





 or ~
or ~


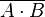 or
or 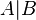


 or
or 


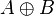


 or
or 